Inference of graph transformation rules for the design of geometric modeling operations
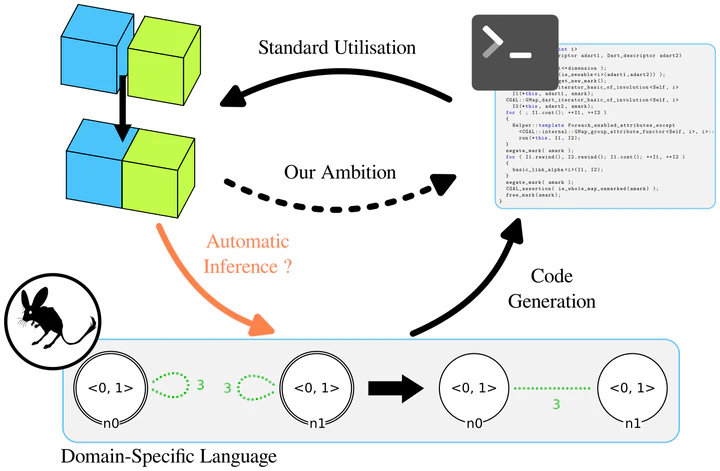 We propose a method to infer graph transformation rules describing geometric modeling operations from a representative example.
We propose a method to infer graph transformation rules describing geometric modeling operations from a representative example.Abstract
In this thesis, we present a formalization of geometric modeling operations as rules from the theory of graph transformation.
First, we investigate the construction of a dedicated rule-based language. We describe the combinatorial models of generalized and oriented maps as labeled graphs, subject to consistency conditions. This topological representation is coupled with a description of the geometry using attributes. This formalization allows the study of modeling operations such as graph rewriting rules. The rules analysis covers two aspects: the preservation of the model consistency and the genericity of the described operations. Consistency preservation is the primary incentive for using graph transformations. Indeed, modifications of a well-formed object should result in a well-formed object. We ensure the preservation of topological and geometric consistency through syntactic conditions statically checked on the rules. In addition, we ensure that rewriting rules meet the requirements to describe the usual operations used in geometric modeling. In particular, since a rule fully describes a transformation, we extend the rules into rule schemes in order to abstract over the underlying topology. We present a semi-global extension of the usual DPO rewriting by incorporating a graph product simulating the application of a relabeling function.
Secondly, we present a mechanism for the inference of operations. Given that an operation can be simply described from a sketch or an example, we propose to reconstruct operations from a representative example made of an initial and a target object. The inference mechanism exploits the regularity of generalized maps and the dedicated language previously. More precisely, we consider the process of inferring topological operations as the inverse construction of the specialization of a rule scheme into an operation. The inference of geometric modifications could admit multiple solutions, given the type of data and the nature of the modifications applied. Here, we propose to consider affine transformations of values from a vector space, which we solve as a constraint satisfaction problem. We have implemented the inference mechanism in Jerboa, a platform for the design of geometric modelers. The first part of this thesis, therefore, allows building a formal framework that is de facto hidden from the user but is still necessary for the conception of geometric modeling operations via our inference mechanism.
Type
Publication
Ph.D. thesis
Compared to the version on these.fr, the present version contains all hyperlinks with color highlights, and the correction of some minor typographical errors pointed out by readers.