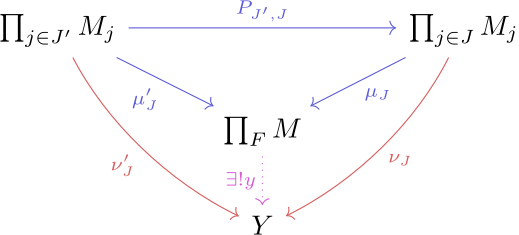
A filtered product of models.
Abstract
In a previous publication, we introduced an abstract logic via an abstract notion of quantifier. Drawing upon concepts from categorical logic, this abstract logic interprets formulas from context as subobjects in a specific category, e.g., Cartesian, regular, or coherent categories, Grothendieck, or elementary toposes. We proposed an entailment system formulated as a sequent calculus which we proved complete. Building on this foundation, our current work explores model theory within abstract logic. More precisely, we generalize one of the most important and powerful classical model theory methods, namely the ultraproduct method, and show its fundamental theorem, i.e., Los’s theorem. The result is shown as independently as possible of a given quantifier.
Romain Pascual
Postdoc
My research interests include applications of graph rewriting to computer graphics, and more generally formal methods from theory to applications.