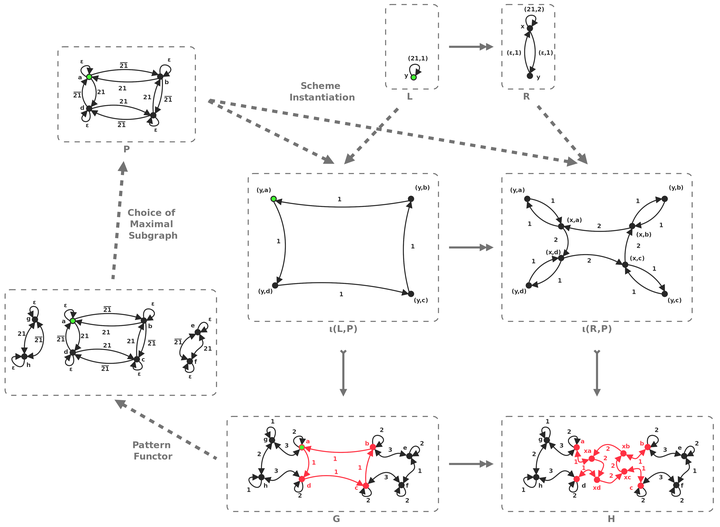
Summary of the process to transform a combinatorial graph with a rule scheme.
Abstract
Topology-based geometric modeling tackles the issue of representing objects with data structures that encode the topological subdivision of modeled objects in vertices, edges, faces, and volumes. Such subdivisions can be represented with graphs labeled by dimensions on arcs, while modeling operations used to edit the objects can be formalized as graph transformations. Among the existing topological models, we consider generalized and oriented maps, defined as constrained labeled graphs, to ensure the well-formedness of the represented objects. Since a modeling operation should provide a correct object when applied to a correct object, graph transformations are provided with conditions to ensure the model consistency. Our approach exploits the firmly established framework of DPO graph transformations to implement modeling operations. We enrich standard DPO graph transformations with a product construction to ease the operation design, enabling generic modeling operations as rule schemes. We lift conditions from DPO rules to this enriched framework, ensuring the preservation of the topological consistency via static analysis of syntactic conditions on rule schemes.
Romain Pascual
Postdoc
My research interests include applications of graph rewriting to computer graphics, and more generally formal methods from theory to applications.