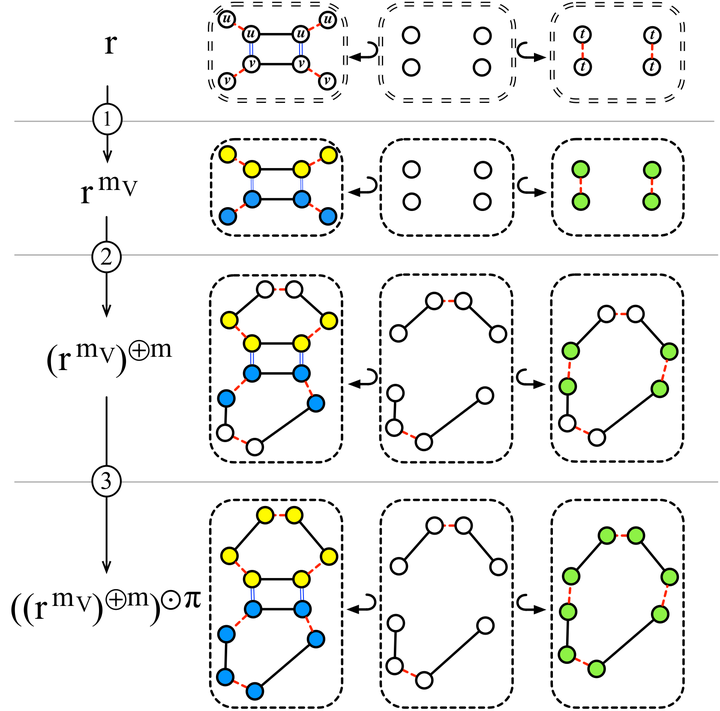
Rule scheme evaluation and instantiation.
Abstract
Labeled graphs are particularly well adapted to represent objects in the context of topology-based geometric modeling. Thus, graph transformation theory is used to implement modeling operations and check their consistency. This article defines a class of graph transformation rules dedicated to embedding computations. Objects are here defined as a particular subclass of labeled graphs in which arc labels encode their topological structure (i.e.,, cell subdivision: vertex, edge, face, etc.) and node labels encode their embedding (i.e., relevant data: vertex positions, face colors, volume density, etc.). Object consistency is defined by labeling constraints which must be preserved by modeling operations that modify topology and/or embedding. Dedicated graph transformation variables allow us to access the existing embedding from the underlying topological structure (e.g., collecting all the points of a face) in order to compute the new embedding using user-provided functions (e.g., compute the barycenter of several points). To ensure the safety of the defined operations, we provide syntactic conditions on rules that preserve the object consistency constraints.
Romain Pascual
Postdoc
My research interests include applications of graph rewriting to computer graphics, and more generally formal methods from theory to applications.