Inferring topological operations on generalized maps: Application to subdivision schemes
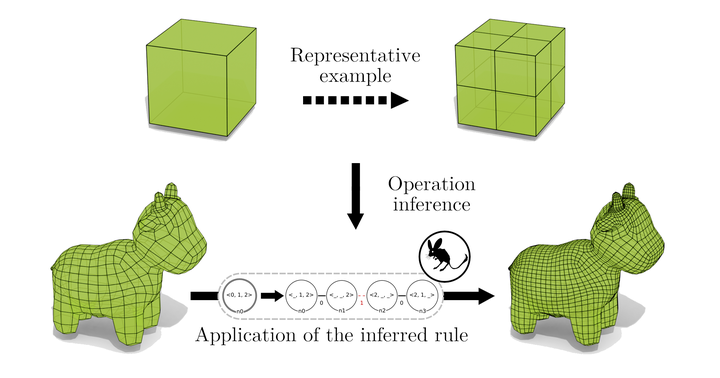 From a representative example (top), we reconstruct an operation applicable in a broader context.
From a representative example (top), we reconstruct an operation applicable in a broader context.
Abstract
The design of correct topological modeling operations is known to be a time-consuming and challenging task. However, these operations are intuitively understood via simple drawings of a representative object before and after modification. We propose to infer topological modeling operations from an application example. Our algorithm exploits a compact and expressive graph-based language. In this framework, topological modeling operations on generalized maps are represented as rules from the theory of graph transformations. Most of the time, operations are generic up to a topological cell (vertex, face, volume). Thus, the rules are parameterized with orbit types indicating which kind of cell is involved. Our main idea is to infer a generic rule by folding a graph comprising a copy of the object before modification, a copy after modification, and information about the modification. We fold this graph according to the cell parameterization of the operation under design. We illustrate our approach with some subdivision schemes because their symmetry simplifies the operation inference.
More information is available on Jerboa’s website.
Demo: