A Note on Los's Theorem for Kripke-Joyal Semantics

Abstract

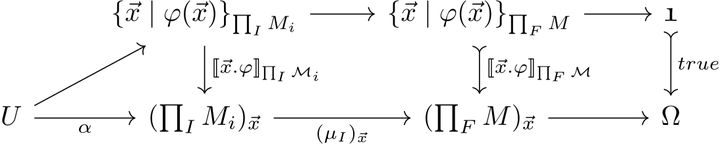
Los’s theorem, also known as the fundamental result of ultraproducts, states that the ultraproduct over a family of structures for the same language satisfies a first-order formula if and only if the set of indices for which the structures satisfy the formula belongs to the underlying ultrafilter. The associated notion of satisfaction is the Tarskian one via the elements of the set-theoretic structure that allow interpreting the formula. In the context of topoi, Kripke-Joyal semantics extends Tarski’s notion to categorical logic. In this article, we propose to extend Los’s theorem to first-order structures on elementary topoi for Kripke-Joyal semantics. We also show that the extension entails its set-theoretic version. As is customary, we use the categorical version of Los’s theorem to obtain a proof of the compactness theorem for Kripke-Joyal semantics.

Romain Pascual

Postdoc

My research interests include applications of graph rewriting to computer graphics, and more generally formal methods from theory to applications.