Instantiation of Jerboa Rule Schemes, a Set-based Explanation

Abstract

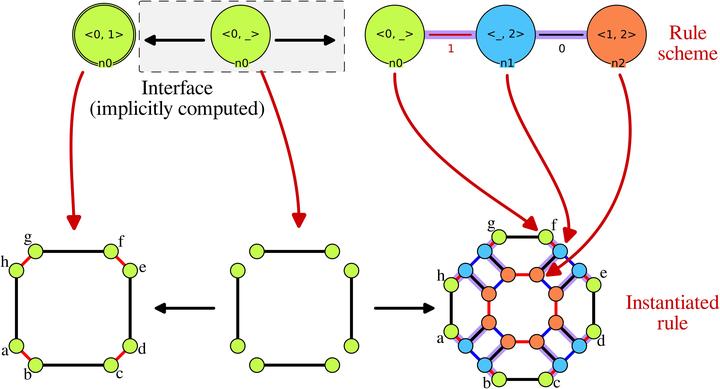
This report presents a set-theoretic framework for the instantiation of rule schemes in the Jerboa platform, a tool for developing domain-specific geometric modelers. Jerboa enables the design of geometric modeling operations as graph transformation rules generalized to rule schemes for genericity over the topological content of the operations. Current approaches to algebraic graph transformations are typically described within a finitary M-adhesive category (where M is a suitable system of monomorphisms), employing compositional double-pushout (DPO) semantics for rewriting. In this report, we propose a lightweight, set-theoretic description that exploits the proximity between presheaf topoi and sets to provide an explanation that does not rely on extensive theoretical background. The proposed method simplifies the formal description of modeling operations to bridge the gap between abstract concepts and their practical application in geometric modeling. The framework offers a complementary perspective to categorical approaches at the foundation of Jerboa.

Romain Pascual

Postdoc

My research interests include applications of graph rewriting to computer graphics, and more generally formal methods from theory to applications.